지난 회에서는 프로그래밍에 있어 단순성의 중요성에 대해 설명하였다. 하지만 그 내용이 다소 추상적으로 기술되었기 때문에, 이번 회에서는 구체적인 프로그래밍 사례(생명 게임)를 통해서 단순성이 실제로 어떻게 프로그램을 단순하게 만드는지에 대해 알아보고자 한다.

(이번 예는 [Clojure Programming]의 ‘Thinking Different: From Imperative to Functional’ 절을 참조하였다.)

콘웨이(Conway)의 생명 게임

생명 게임은 영국의 수학자 존 호톤 콘웨이(John Horton Conway)가 만든 세포 자동자의 일종인데,  몇가지 간단한 규칙만으로 복잡한 패턴을 만들어 내는 특징이 있다. 생명 게임은 초기값에 따라 그 진화하는 방식이 매우 다양해진다는 점 때문에 많은 사람들의 관심과 호응을 불러 일으켰다.

생명 게임의 규칙은 다음과 같이 4개의 규칙으로 되어 있다.

1. 산 세포의 이웃 중 산 세포가 2개 미만이면 다음 세대에 죽는다. (인구부족 요인)
2. 산 세포의 이웃 중 산 세포가 2, 3개이면 다음 세대에 산다.
3. 산 세포의 이웃 중 산 세포가 3개 초과이면 다음 세대에 죽는다. (인구과잉 요인)
4. 죽은 세포 중 살아있는 이웃이 3개이면 다음 세대에 산다. (재탄생 요인)

생명 게임은 많은 패턴을 만들어낸다고 했는데, 그 중 우리는 특히 글라이더(glider)라고 이름 붙여진 패턴을 만들어 볼 것이다. 우선 위 규칙이 어떻게 적용되는지 알아보자.

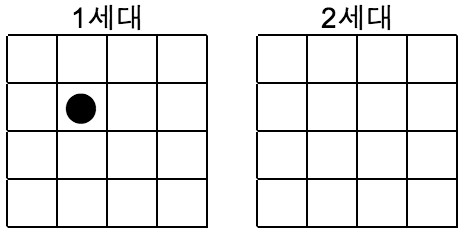
다음과 같이 ‘⬤’로 표시된 칸은 산 세포이고, 아무 표시가 없는 칸은 죽은 세포이다. 현재 1세대에는 산 세포는 하나 밖에 없다. 하지만 이 산 세포는 이웃 세포 중 살아있는 세포가 없기 때문에 규칙 1 (인구부족 요인)에 따라 다음 세대에서 죽는다. 다른 칸들은 모두 죽은 세포들인데 규칙 4 (재탄생 요인)에 따라 산 세포가 되기 위한 살아있는 이웃 세포 3개가 없기 때문에 역시 죽은 채로 그대로 남게 된다. 결국 모든 칸에 다음 세대에 살아남는 세포는 없다. 2 세대에는 모두 죽은 세포만 있으므로 더 이상 세대는 없다.

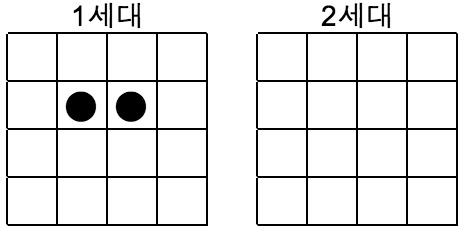
다음은 산 세포가 2개 있는 경우이다. 이 경우에도 위와 같이 산 세포들은 규칙 1 (인구부족 요인)의 적용을 받아 죽게 되고, 죽은 세포 중 살게 되는 경우도 없어 2 세대에는 살아남은 세포가 없다.

다음은 3개의 산 세포가 있는 경우이다. 1 세대에서 산 세포들은 각각 2개의 산 세포를 이웃으로 갖게 되므로 규칙 2에 따라 다음 세대에 살아남게 된다. 한편 죽은 세포들 중 (1, 3) 칸은 살아있는 세포가 주위에 3개가 있기 때문에 규칙 4 (재탄생 요인) 에 의해 다음 세대에 되살아나게 된다. 그래서 2 세대에서는 산 세포가 4개로 증가하게 된다. 2 세대에서는 살아있는 세포들은 모두 3개의 산 이웃 세포 갖기 때문에 규칙 2에 의해 계속 살아남게 되고, 죽은 세포들은 규칙 4에 의해 그대로 남게된다. 결국 3 세대에도 똑같은 패턴이 나오게 된다.

다음의 패턴은 독자분들께서 직접 규칙을 적용해 볼 수 있을 것이다.

이제 글라이더 패턴을 보자. 글라이더 패턴은 아래 3개 모양을 반복하면서 사선 방향으로 진행하게 된다. 그래서 글라이더라고 이름을 붙였다.

아래는 글라이더가 진행되는 모습을 보이고 있다.

(콘웨이의 생명 게임에서 더 많은 패턴들은 다음 링크를 보라 : 다양한 패턴들)

클로저로 구현하기

이제 생명 게임의 규칙에 대해서 알게 되었을 것이다. 이것을 클로저 코드로 표현해 보자. 우리는 여기서 2가지 방식으로 구현된 코드를 살펴볼 것이다. 하나는 복잡한 코드이고, 다른 하나는 단순한 코드이다. 우선 먼저 단순한 코드부터 살펴 볼 것이다. (본 글에서는 전체 소스 중 일부 핵심 부분만 발췌해서 살펴본다. 전체 소스를 보고 싶다면 다음 링크를 확인해 보라.  전체 구현 소스)

그 전에 양쪽 코드에서 공통으로 사용되는 함수를 보자.

(defn neighbours [[x y]]
 (for [dx [-1 0 1] dy [-1 0 1] :when (not= 0 dx dy)]
   [(+ dx x) (+ dy y)]))

클로저에서 defn은 함수를 정의한다. neighbours 함수는 현재 좌표 [x y] 에서의 이웃 세포들의 좌표를 만들어 내는 함수이다. 좌표 [1 1]의 이웃 좌표들은 다음과 같다.

(neighbours [1 1])
;=> ([0 0] [0 1] [0 2] [1 0] [1 2] [2 0] [2 1] [2 2])

다음은 생명 게임 구현한 단순한 코드이다.

코드 1 : 단순한 코드

(defn step  [cells]
 (set (for [[loc n] (frequencies (mapcat neighbours cells))
                :when (or (= n 3) (and (= n 2) (cells loc)))]
          loc)))

다음은 복잡한 코드이다.

코드 2: 복잡한 코드

(defn count-neighbours
 [board loc]
 (count (filter #(get-in board %) (neighbours loc))))

(defn step [board]
 (let [w (count board)
        h  (count (first (board))]
   (loop [new-board board x 0 y 0]
     (cond
        (>= x w) new-board
        (>= y h) (recur new-board (inc x) 0)
        :else
          (let [new-liveness
                   (case (count-neighbours board [x y])
                     2 (get-in board [x y])  
                     3 :on
                     nil)]
             (recur (assoc-in new-board [x y] new-liveness) x (inc y)))))))

단순한 코드 1은 4줄인데 비해 복잡한 코드 2는 무려 18줄이다. 이 차이가 놀라울 따름이다. 도대체 왜 이런 차이가 발생한 것일까? 코드 2가 왜 이리 복잡해졌을까? 그 이유를 알아보자.

코드 1 설명

먼저 defn 키워드로 step 함수를 정의하고 있다(1째줄). 이 함수는 세대를 말하는 것으로 현재 세대가 입력이고 다음 세대가 출력이다. cells는 step 함수의 파라미터로, 현재 세대의 살아있는 세포들의 좌표이다. 앞서 neighbours 함수는 cell의 이웃 세포들 좌표들을 만든다고 했다. 2째줄의 for문이 하는 역할은 살아있는 세포들 cells 마다 각각의 이웃들의 좌표를 나열(mapcat)해서, 중복으로 겹쳐 나타나는 좌표들의 빈도(frequencies)를 구하는 것이다. 이렇게 중복으로 나타난 좌표의 빈도수가 사실은 그 중복된 좌표에서의 살아있는 이웃 세포의 수가 된다.  즉 살아있는 세포를 이웃으로 하는 좌표(loc)를 중심으로 해서 과연 살아있는 세포가 몇 개(n)인지를 알게 되는 것이다. 그후 3째 줄에서는 다음 조건이 맞을 때(:when)의 loc만을 리턴한다. 즉 살아있는 이웃이 3개 (= n 3)이거나 혹은 살아있는 이웃이 2개 (= n 2)인데 그 좌표(loc)가 살아있는 세포인(cells loc) 경우.

코드 2 설명

다음으로 코드 2를 보자.  우선 count-neighbours함수는 파라미터 loc 좌표에서의 살아있는 이웃의 갯수를 리턴하는 함수이다. indexed-step 함수는 파라미터로 board를 받고 있다(4째줄). 보드의 너비와 높이는 w와 h로 받는다(5, 6째줄). loop문과 17 째줄의 recur는 루프문을 이루면서 x, y 좌표를 증가시켜 가며 board의 각 셀을 순회한다. 8, 9, 10째줄의 cond 절은 좌표 x, y가 보드의 너비(w)와 높이(h)를 넘지 않도록 값을 한정한다. 핵심적인 부분은 let 절이다. case 구문에서는 board의 [x y] 좌표의 살아있는 이웃의 수를 센 후, 그 수가 2인 경우는 board의 [x y] 좌표에 해당하는 값을, 3인 경우는 살아있음(:on)을, 그외의 경우에는 nil을 new-liveness가 받는다. (12~16 줄). 17째 줄에서는 let절에서 계산된 해당 좌표의 다음 세대 값(new-liveness)을 보드에 기록한다.

코드 비교

먼저 생명 게임 규칙을 다시 살펴보자. 규칙을 보면 몇가지 단어들이 나타난다. 이웃, 산 세포, 죽은 세포, 세대, 2, 3 등. 즉 인간의 언어로 표현된 생명 게임의 규칙들에는 이런 단어들 밖에 없다.

코드 1을 보면 step, cells, neighbours, 2, 3이라는 단어들이 나타나는 것을 볼 수 있는데, 이는 인간의 언어로 기술된 생명 게임 규칙의 세대, 세포, 이웃, 2, 3과 일치하는 단어들이다. 그 외에 생명 게임 규칙에는 없던 단어들은 frequencies, mapcat, for, set, loc, n 등 정도이다. 이 단어들은 이웃을 세는 행위를 나타내기 위해 필요한 것이다. 코드 1은 인간의 언어로 표현한 것과 거의 정확하게 기술하고 있다. 군더더기가 거의 없다.

반면 코드 2를 보자. 여기서는 인간의 언어에도, 코드 1에도 없던 단어들이 눈에 많이 뛴다. board, x, y, w, h, loop, cond, case, get-in, assoc-in 등. 이 단어들은 코드 2의 step함수가 파라미터를 board로 받으면서 어쩔 수 없이 board를 순회하기 위해 따라 나올 수 밖에 없는 것들이다.

결국 코드 1과 코드 2의 차이는 step 함수의 파라미터가 cells인가 board인가에서 결정되는 것이다.

하지만 생명 게임 규칙에서는 board라는 개념은 등장하지 않는다. 원래 생명 게임 규칙은 인간의 언어로 기술되었고, 그 기술된 바 대로 기계적으로 수행하면 생명 게임이 되는 것이다. 이것을 인간의 언어가 아닌 프로그래밍 언어로 바꾸는데 있어 코드 1과 코드 2가 저렇게 큰 차이가 난 이유는 원래 생명 게임 규칙에는 없는 개념인 board라는 개념이 코드 2에 추가되었고 이를 표현하려다 보니 코드의 크기가 커진 것이다. 사실 인간의 언어로 작성된 생명 게임 규칙 자체가 board라는 개념 없이도 충분히 프로그램화 될 수 있다는 것을 보여주고 있는데 말이다.

그런데 왜 board라는 개념이 들어왔을까?

인위적 식별자와 자연적 식별자

코드 2가 코드 1에 비해 복잡했던 이유는 board라는 개념이 끼어들었기 때문이라는 것을 알았다. 왜 이런 개념이 끼어들게 되었을까?

명령형 프로그래밍에 익숙한 우리는 인덱스를 통해 무언가를 참조하는데 매우 익숙하다 (예를 들어 배열의 인덱스나 포인터). 코드 2에서 좌표 [x y]는 정확하게 인덱스로 사용되고 있는데, 이를 통해 지칭하고자 하는 것은 board에서의 그 좌표 [x y]에 위치한 값이다 (:on 혹은 nil). 우리는 이렇게 board를 [x y]라는 좌표로 순회하는 데 매우 익숙한데, 이런 익숙함은 손쉽게 board라는 개념으로 우리를 이끌었던 것이다.

하지만 코드 1에서 좌표는 결코 [x y] 형태로 나타나지 않는다. 코드 1에서도 코드 2에서처럼 neighbours 함수가 사용되고는 있지만, 좌표는 무엇인가를 지칭하기 위해서 사용된 것이 아니라 그 자체를 값으로서 사용되고 있는데, 즉 같은 좌표가 몇 번 나타났는지에 대한 빈도를 얻기 위해서만이지, 그 좌표에 있는 board내의 값에 접근하기 위해서가 아니다.

이것을 좀 더 명확하게 얘기하면, 좌표는 코드 1에서는 자연적 식별자이고, 코드 2에서는 인위적 식별자라고 할 수 있다. 식별이라는 말은 무엇인가를 다른 것과 구별해서 인식한다는 것이다. 자연적 식별자란 순수한 값 그 자체가 자기 자신을 식별한다는 것을 말한다. 즉 1과 2를 식별하는 것은 1과 2 그 자체라는 것이다. 반면 인위적 식별자는 다른 값을 식별하기 위한 값, 혹은 매핑을 말한다. 즉 1과 2를 식별하기 위해 1은 one으로, 2는 two로 대신 지칭하는 것과 같다.

자연적 식별자

• 순수한 값 그 자체는 자기 자신을 식별한다.
• 1은 1 자신을 식별한다.
• 값은 그 자체로 식별자로서 충분하다.

인위적 식별자

• 다른 값을 식별하기 위한 값.
• 매핑.
• 정수 1을 식별하기 위한 Integer 1.
• 데이타베이스의 자동 증가 ID.
• 복잡성을 야기

인위적 식별자는 기본적으로 자연적 식별자보다 더 복잡한 개념이다. 왜냐면 인위적 식별자는 원래의 값과 그것을 참조하는(가리키는) 값이 하나 더 있기 때문이다. 복잡한 개념을 사용하게 되면 코드 역시 더 복잡해진다. 코드 2가 복잡해진 이유는 좌표를 자연적 식별자보다 복잡한 개념인 인위적 식별자로 사용했기 때문이다.

단순성과 디자인

사실 코드 2는 코드 1에 비해 더 많은 일을 한다. 코드 1의 step 함수는 다음 세대의 살아있는 세포의 좌표만을 리턴할 뿐이지만, 코드 2의 indexed-step 함수는 다음 세대의 살아있는 세포를 board에 기록하고 있다. 전체 구현 코드를 보면 코드 1의 step 함수의 결과를 받아 board에 기록하는 populate함수가 있다.

(defn populate [board living-cells]
  (reduce (fn [board coordinates]
                (assoc-in board coordinates :on))
               board
              living-cells))

코드 1에서는 다음 세대의 살아있는 세포만을 구하는 step 함수와 그것을 board에 기록하는 populate 함수가 분리되어 있는 반면, 코드 2에서는 이 2 개의 기능이 indexed-step 함수에 뒤엉켜서 구현되어 있는 것이다. 디자인의 관점에서 봤을 때 이것은 SoC(Seperation of Concerns)의 원리를 위반하는 것이다. 인위적 식별자를 기반으로 하는 코드는  SoC를 위반하도록 만든다.  자연적 식별자를 우선시 한다는 것은 핵심적 요소를 분리하고 거기에 초점을 집중하는 것을 말한다.

단순함이 주는 확장성

코드 1은 자연적 식별자를 사용함으로써 step 함수가 오직 산 세포에만 관심에 집중하게 되는데, 이것의 이점은 코드가 짧아졌다는 것 이상이다. 코드가 단순해지면 쉽게 확장할 수 있게 된다.

코드 1에서 step 함수가 좌표를 순수하게 값 그 자체으로서만 사용하기 때문에, 그래서 한편으로 neighbours 함수는 좌표의 외적 요소(좌표와 좌표와의 관계, 즉 좌표가 누군가의 이웃인지)에 관심을 갖는 유일한 함수가 되는데, 이웃임을 결정하는 것은 좌표 평면에 의해 결정되기 때문에, 좌표가 평면 기하면에 있던지, 구부러진 표면에 있던지, 아니면 벌집 모양이던지는 neighbours 함수에만 관계된 것이지 step 함수와는 상관없는 일이 된다. 결국 neighbours 함수만 해당 평면에 맞추어 고쳐주기만 하면 step 함수는 수정하지 않아도 코드 1은 쉽게 해당 평면에 대한 생명 게임을 구현할 수 있게 된다.

(defn hex-neighbours [[x y]]
 (for [dx [-1 0 1] dy (if (zero? dx) [-2 2] [-1 1])]
   [(+ dx x) (+ dy y)]))

hex-neighbours 함수는 평면이 사각형의 칸이 아니라 육각형 칸으로 구성된 벌집 모양일때 이웃 세포의 좌표를 구하는 함수이다. step 함수는 좌표의 빈도에만 관여하기 때문에 step 함수에서 사용되었던 neighbours 함수는 hex-neighbours 함수로 바로 교체될 수 있다.

교훈

클로저로 생명 게임을 구현할 때 단순하게도 혹은 복잡하게도 구현할 수 있음을 알았다. 클로저가 단순한 코드를 만들도록 보장해 주지는 않는다. 다만 클로저는 단순한 코드를 쉽게 짤 수 있도록 도와준다는 것이다. 자바로도 단순한 코드를 짤 수 있을 것이지만, 자바로 단순한 코드를 짠다는 것은 어셈블리로 객체지향 프로그래밍을 하는 것과 같은 정도로 결코 쉬운 일이 아니다.

클로저는 그 언어의 설계 자체가 단순성에 최대의 역점을 두었다.  이러한 점 때문에 클로저는 다른 언어들에 비해서 우연적 복잡성이 가미될 소지가 현저하게 줄어들게 된다. 다음 회에서는 클로저가 어떻게 단순하게 설계되었는지 프로그래밍 패러다임적 관점에서 살펴볼 것이다.